Lesson 3 - B-Trees
B-Tree was developed in the year of 1972 by Rudolf Bayer and McCreight with the name Height Balanced m-way Search Tree. Later it was named as B-Tree.
B-Trees are:
- Balanced
- It is a self balancing data structure, which means that performance can be guaranteed when B-Trees are utilised.
- Broad
- As opposed to binary search trees, which grow vertically, B-Trees expand horizontally
A B-tree is a specialised multiway tree designed especially for use on disk. In a B-tree each node may contain a large number of keys. The number of subtrees of each node, then, may also be large. A B-tree is designed to branch out in this large number of directions and to contain a lot of keys in each node so that the height of the tree is relatively small. This means that only a small number of nodes must be read from disk to retrieve an item. The goal is to get fast access to the data, and with disk drives this means reading a very small number of records. Note that a large node size (with lots of keys in the node) also fits with the fact that with a disk drive one can usually read a fair amount of data at once.
A multiway tree of order m is an ordered tree where each node has at most m children. For each node, if k is the actual number of children in the node, then k - 1 is the number of keys in the node. If the keys and subtrees are arranged in the fashion of a search tree, then this is called a multiway search tree of order m. For example, the following is a multiway search tree of order 4. Note that the first row in each node shows the keys, while the second row shows the pointers to the child nodes. Of course, in any useful application there would be a record of data associated with each key, so that the first row in each node might be an array of records where each record contains a key and its associated data. Another approach would be to have the first row of each node contain an array of records where each record contains a key and a record number for the associated data record, which is found in another file. This last method is often used when the data records are large.
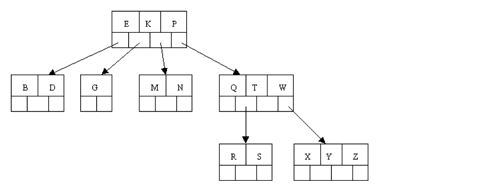
Properties
B-Tree of Order m has the following properties:- All the leaf nodes must be at same level.
- All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.
- All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
- If the root node is a non leaf node, then it must have at least 2 children.
- A non leaf node with n-1 keys must have n number of children.
- All the key values within a node must be in ascending order.
template <typename Data>
struct Node
{
uint16_t count; // number of keys stored in the current node
Data key[3]; // array to hold the 3 keys
uint64_t branch[4]; // array of fake pointers (record numbers)
};
With a simple structure as above used to denote a node, a multiway search tree of order 4 has to fulfil the following conditions related to the ordering of the keys:
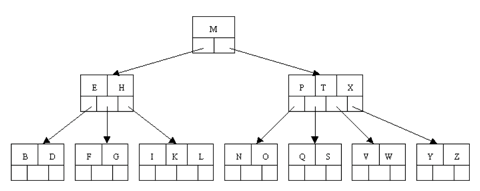
The following is an example of a B-tree of order 5. This means that (other that the root node) all internal nodes have at least (5 / 2) + 1 = 3 children (and hence at least 2 keys). The maximum number of children that a node can have is 5 (so 4 is the maximum number of keys). Each leaf node must contain at least 2 keys. In practice B-trees usually have orders a lot bigger than 5.
B-Trees support the same types of operations that binary trees did - search, insert and remove.
Search operation is similar to that of Binary Search Tree. In a Binary search tree, the search process starts from the root node and each time we make a 2-way decision (we go to either left subtree or right subtree). Similarly in a B-Tree search process starts from the root node but each time we make an n-way decision, where n is the total number of children that node has. In a B-Tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows:
The insertion algorithm proceeds as follows:
The above mentioned technique is sometimes referred to as the reactive technique. An alternative technique called the proactive technique splits any full node as soon as it is encountered in the search for the location in which the item is to be added. The proactive technique has the benefit that the algorithm will visit the nodes only once in cases where split(s) are required. The reactive technique on the other hand may need to revisit the parent nodes all the way to the root when splits are required depending on whether the parent node are full. The proactive technique suffers from the downside that it will split a parent node regardless of whether a child node to which the item will be attached is full or not (in other words may split when a split is not absolutely needed).
Let's work our way through an example. Insert the following letters into what is originally an empty B-tree of order 5:
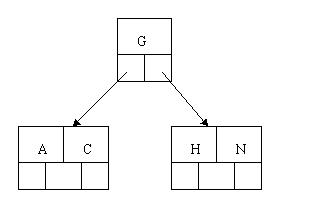
When we try to insert the H, we find no room in this node, so we split it into 2 nodes, moving the median item G up into a new root node. Note that in practice we just leave the A and C in the current node and place the H and N into a new node to the right of the old one.
Inserting E, K, and Q proceeds without requiring any splits:
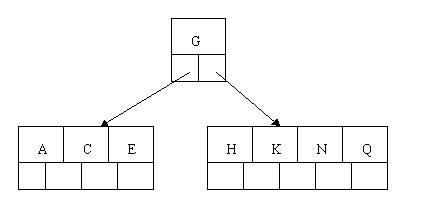
Inserting M requires a split. Note that M happens to be the median key and so is moved up into the parent node.
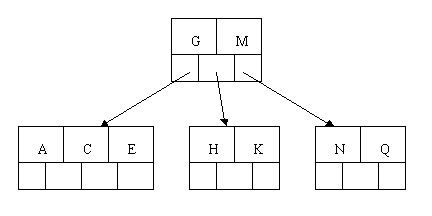
The letters F, W, L, and T are then added without needing any split.
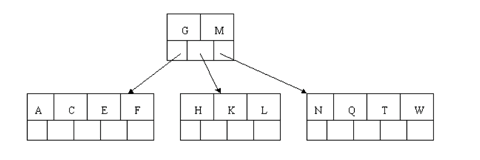
When Z is added, the rightmost leaf must be split. The median item T is moved up into the parent node. Note that by moving up the median key, the tree is kept fairly balanced, with 2 keys in each of the resulting nodes.
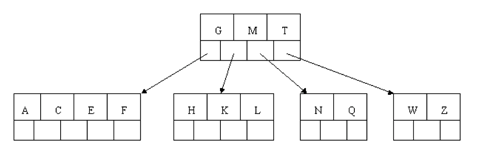
The insertion of D causes the leftmost leaf to be split. D happens to be the median key and so is the one moved up into the parent node. The letters P, R, X, and Y are then added without any need of splitting:
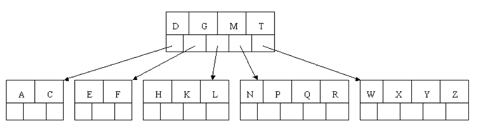
Finally, when S is added, the node with N, P, Q, and R splits, sending the median Q up to the parent. However, the parent node is full, so it splits, sending the median M up to form a new root node. Note how the 3 pointers from the old parent node stay in the revised node that contains D and G.
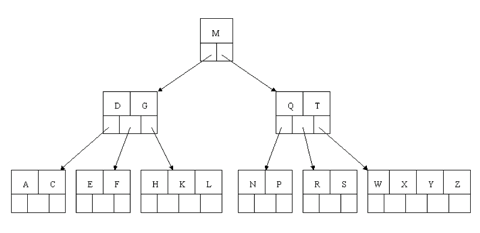
In the B-tree as we left it at the end of the last section, delete H. Of course, we first do a lookup to find H. Since H is in a leaf and the leaf has more than the minimum number of keys, this is easy. We move the K over where the H had been and the L over where the K had been. This gives:
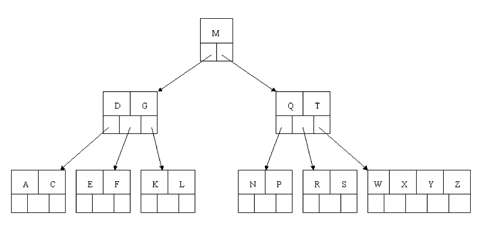
Next, delete T. Since T is not in a leaf, we find its successor (the next item in ascending order), which happens to be W, and move W up to replace the T. That way, what we really have to do is to delete W from the leaf, which we already know how to do, since this leaf has extra keys. In all cases we reduce deletion to a deletion in a leaf, by using this method.
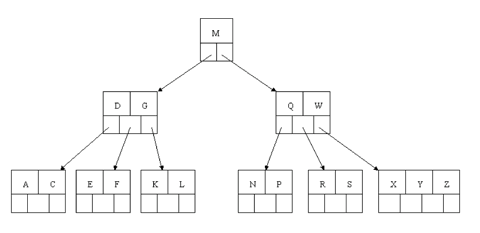
Next, delete R. Although R is in a leaf, this leaf does not have an extra key; the deletion results in a node with only one key, which is not acceptable for a B-tree of order 5. If the sibling node to the immediate left or right has an extra key, we can then borrow a key from the parent and move a key up from this sibling. In our specific case, the sibling to the right has an extra key. So, the successor W of S (the last key in the node where the deletion occurred), is moved down from the parent, and the X is moved up. (Of course, the S is moved over so that the W can be inserted in its proper place.)
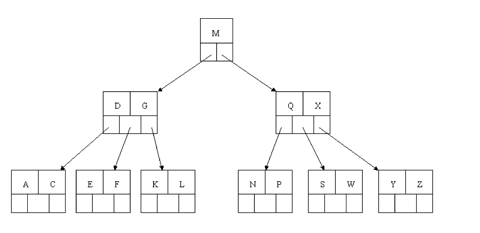
Finally, let's delete E. This one causes lots of problems. Although E is in a leaf, the leaf has no extra keys, nor do the siblings to the immediate right or left. In such a case the leaf has to be combined with one of these two siblings. This includes moving down the parent's key that was between those of these two leaves. In our example, let's combine the leaf containing F with the leaf containing A C. We also move down the D.
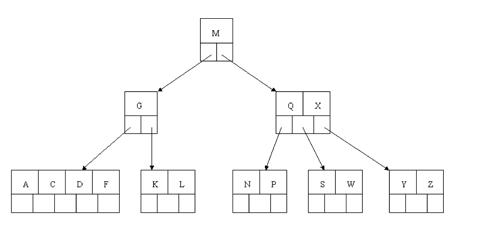
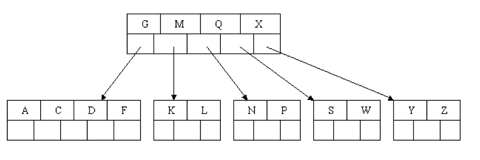
Of course, you immediately see that the parent node now contains only one key, G. This is not acceptable. If this problem node had a sibling to its immediate left or right that had a spare key, then we would again "borrow" a key. Suppose for the moment that the right sibling (the node with Q X) had one more key in it somewhere to the right of Q. We would then move M down to the node with too few keys and move the Q up where the M had been. However, the old left subtree of Q would then have to become the right subtree of M. In other words, the N P node would be attached via the pointer field to the right of M's new location. Since in our example we have no way to borrow a key from a sibling, we must again combine with the sibling, and move down the M from the parent. In this case, the tree shrinks in height by one.
Many data structures, such as binary search trees were created to be stored in memory. However B-Trees have a different purpose. They focus on large amounts of data. The typical usage for B-Trees in applications is for database indices.
If you’ve never used a database index before, an index is essentially a copy of a database column that allows for fast queries for common searches. For example, if you have a database table that stores users, you can use an index to quickly search for users by their email address.
Since information such as a list of users would be too difficult to store in memory, B-Trees allow for rapid searches on external hard disks, such as in database files.
http://btechsmartclass.com/DS/U5_T3.html
https://www.crondose.com/2016/10/introduction-to-the-b-tree-data-structure/
http://cis.stvincent.edu/html/tutorials/swd/btree/btree.html
https://github.com/Tessil/hat-trie
- The keys in each node are in ascending order.
- At every given node the following is true:
- The subtree starting at record Node.branch[0] has only keys that are less than Node.key[0].
- The subtree starting at record Node.branch[1] has only keys that are greater than Node.key[0] and at the same time less than Node.key[1].
- The subtree starting at record Node.branch[2] has only keys that are greater than Node.key[1] and at the same time less than Node.key[2].
- The subtree starting at record Node.branch[3] has only keys that are greater than Node.key[2].
- Note that if less than the full number of keys are in the Node, these 4 conditions are truncated so that they speak of the appropriate number of keys and branches.
Example
The following is an example of a B-tree of order 5. This means that (other that the root node) all internal nodes have at least (5 / 2) + 1 = 3 children (and hence at least 2 keys). The maximum number of children that a node can have is 5 (so 4 is the maximum number of keys). Each leaf node must contain at least 2 keys. In practice B-trees usually have orders a lot bigger than 5.

Operations
B-Trees support the same types of operations that binary trees did - search, insert and remove.
Search
Search operation is similar to that of Binary Search Tree. In a Binary search tree, the search process starts from the root node and each time we make a 2-way decision (we go to either left subtree or right subtree). Similarly in a B-Tree search process starts from the root node but each time we make an n-way decision, where n is the total number of children that node has. In a B-Tree, the search operation is performed with O(log n) time complexity. The search operation is performed as follows:
- Compare the search value with first key value of root node in the tree.
- If it matches, return the matching node.
- If it does not match, check whether search element is smaller or larger than that key value.
- If search element is smaller, then continue the search process in left subtree.
- If search element is larger, then compare with next key value in the same node and repeat step 2, 3, 4 and 4 until we found exact match or comparison completed with last key value in a leaf node.
- If we completed with last key value in a leaf node the tree did not contain the specified value
Insert
The insertion algorithm proceeds as follows:
- Perform a search for it in the B-tree.
- If the item is not already in the B-tree, this unsuccessful search will end at a leaf.
- If there is room in this leaf, just insert the new item here. Note that this may require that some existing keys be moved one to the right to make room for the new item.
- If this leaf node is full the node must be "split" with about half of the keys going into a new node to the right of this one.
- The median (middle) key is moved up into the parent node. (Of course, if that node has no room, then it may have to be split as well.)
- Note that when adding to an internal node, not only might we have to move some keys one position to the right, but the associated pointers have to be moved right as well.
- If the root node is ever split, the median key moves up into a new root node, thus causing the tree to increase in height by one.
Note
The above mentioned technique is sometimes referred to as the reactive technique. An alternative technique called the proactive technique splits any full node as soon as it is encountered in the search for the location in which the item is to be added. The proactive technique has the benefit that the algorithm will visit the nodes only once in cases where split(s) are required. The reactive technique on the other hand may need to revisit the parent nodes all the way to the root when splits are required depending on whether the parent node are full. The proactive technique suffers from the downside that it will split a parent node regardless of whether a child node to which the item will be attached is full or not (in other words may split when a split is not absolutely needed).
Let's work our way through an example. Insert the following letters into what is originally an empty B-tree of order 5:
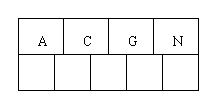
C N G A H E K Q M F W L T Z D P R X Y S. Order 5 means that a node can have a maximum of 5 children and 4 keys. All nodes other than the root must have a minimum of 2 keys. The first 4 letters get inserted into the same node, resulting in this picture:
When we try to insert the H, we find no room in this node, so we split it into 2 nodes, moving the median item G up into a new root node. Note that in practice we just leave the A and C in the current node and place the H and N into a new node to the right of the old one.

Inserting E, K, and Q proceeds without requiring any splits:

Inserting M requires a split. Note that M happens to be the median key and so is moved up into the parent node.

The letters F, W, L, and T are then added without needing any split.

When Z is added, the rightmost leaf must be split. The median item T is moved up into the parent node. Note that by moving up the median key, the tree is kept fairly balanced, with 2 keys in each of the resulting nodes.

The insertion of D causes the leftmost leaf to be split. D happens to be the median key and so is the one moved up into the parent node. The letters P, R, X, and Y are then added without any need of splitting:

Finally, when S is added, the node with N, P, Q, and R splits, sending the median Q up to the parent. However, the parent node is full, so it splits, sending the median M up to form a new root node. Note how the 3 pointers from the old parent node stay in the revised node that contains D and G.

Delete
In the B-tree as we left it at the end of the last section, delete H. Of course, we first do a lookup to find H. Since H is in a leaf and the leaf has more than the minimum number of keys, this is easy. We move the K over where the H had been and the L over where the K had been. This gives:

Next, delete T. Since T is not in a leaf, we find its successor (the next item in ascending order), which happens to be W, and move W up to replace the T. That way, what we really have to do is to delete W from the leaf, which we already know how to do, since this leaf has extra keys. In all cases we reduce deletion to a deletion in a leaf, by using this method.

Next, delete R. Although R is in a leaf, this leaf does not have an extra key; the deletion results in a node with only one key, which is not acceptable for a B-tree of order 5. If the sibling node to the immediate left or right has an extra key, we can then borrow a key from the parent and move a key up from this sibling. In our specific case, the sibling to the right has an extra key. So, the successor W of S (the last key in the node where the deletion occurred), is moved down from the parent, and the X is moved up. (Of course, the S is moved over so that the W can be inserted in its proper place.)

Finally, let's delete E. This one causes lots of problems. Although E is in a leaf, the leaf has no extra keys, nor do the siblings to the immediate right or left. In such a case the leaf has to be combined with one of these two siblings. This includes moving down the parent's key that was between those of these two leaves. In our example, let's combine the leaf containing F with the leaf containing A C. We also move down the D.

Of course, you immediately see that the parent node now contains only one key, G. This is not acceptable. If this problem node had a sibling to its immediate left or right that had a spare key, then we would again "borrow" a key. Suppose for the moment that the right sibling (the node with Q X) had one more key in it somewhere to the right of Q. We would then move M down to the node with too few keys and move the Q up where the M had been. However, the old left subtree of Q would then have to become the right subtree of M. In other words, the N P node would be attached via the pointer field to the right of M's new location. Since in our example we have no way to borrow a key from a sibling, we must again combine with the sibling, and move down the M from the parent. In this case, the tree shrinks in height by one.

Applications
Many data structures, such as binary search trees were created to be stored in memory. However B-Trees have a different purpose. They focus on large amounts of data. The typical usage for B-Trees in applications is for database indices.
If you’ve never used a database index before, an index is essentially a copy of a database column that allows for fast queries for common searches. For example, if you have a database table that stores users, you can use an index to quickly search for users by their email address.
Since information such as a list of users would be too difficult to store in memory, B-Trees allow for rapid searches on external hard disks, such as in database files.
References
http://btechsmartclass.com/DS/U5_T3.html
https://www.crondose.com/2016/10/introduction-to-the-b-tree-data-structure/
http://cis.stvincent.edu/html/tutorials/swd/btree/btree.html
https://github.com/Tessil/hat-trie
