Lesson 2 - Tree Balancing
Search performance across a binary search tree is proportional to the height of the tree. We have also seen that adding data in sequence to a non-self balancing tree degenerates into a linked list leading to poor (linear) search performance. Numerous techniques have been developed to balance binary trees. Some of the approaches involve constant re-balancing (on insert as in AVL and R-B trees, on each read in Splay trees) in an effort to ensure near optimal search performance.
Note that re-balancing is an expensive process and the overall performance characteristic of a tree is heavily influenced by the number or re-balancing operations required while the tree is in use.
Tree Rotation
Most self balancing trees use a common rotation system to re-balance the tree. Tree rotation is an operation on a binary tree that changes the structure without interfering with the order of the elements. A tree rotation moves one node up in the tree and one node down. It is used to change the shape of the tree, and in particular to decrease its height by moving smaller subtrees down and larger subtrees up, resulting in improved performance of many tree operations.
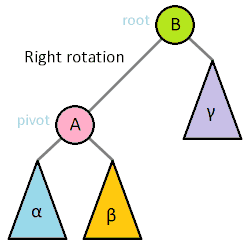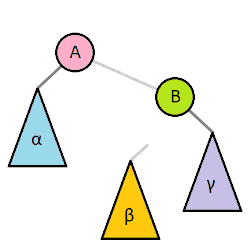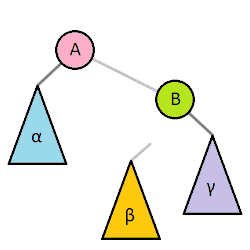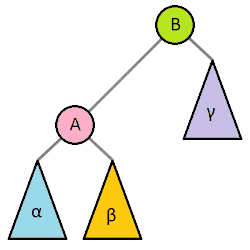
When a subtree is rotated, the subtree side upon which it is rotated increases its height by one node while the other subtree decreases its height. This makes tree rotations useful for rebalancing a tree. The tree rotation renders the inorder traversal of the binary tree invariant. This implies the order of the elements are not affected when a rotation is performed in any part of the tree.
A tree can be rebalanced using rotations. After a rotation, the side of the rotation increases its height by 1 whilst the side opposite the rotation decreases its height similarly. Therefore, one can strategically apply rotations to nodes whose left child and right child differ in height by more than 1.
Splay Tree
A splay tree is a self-adjusting binary search tree with the additional property that recently accessed elements are quick to access again. It performs basic operations such as insertion, look-up and removal in O(log n) amortised time. For many sequences of non-random operations, splay trees perform better than other search trees, even when the specific pattern of the sequence is unknown.
Splaying
When a node x is accessed, a splay operation is performed on x to move it to the root. To perform a splay operation we carry out a sequence of splay steps, each of which moves x closer to the root. By performing a splay operation on the node of interest after every access, the recently accessed nodes are kept near the root and the tree remains roughly balanced, so that we achieve the desired amortised time bounds.
Each particular step depends on three factors:
- Whether x is the left or right child of its parent node, p
- whether p is the root or not, and if not
- whether p is the left or right child of its parent, g (the grandparent of x).
It is important to remember to set gg (the great-grandparent of x) to now point to x after any splay operation. If gg is null, then x obviously is now the root and must be updated as such.
There are three types of splay steps, each of which has a left- and right-handed case.
- Zig (or Zag): Node is child of root (the node has no grandparent). Node is either a left child of root (we do a right rotation - zig) or node is a right child of its parent (we do a left rotation - zag).

- Node has both parent and grandparent. There can be following subcases.
- Zig-Zig and Zag-Zag. Node is left child of parent and parent is also left child of grand parent (Two right rotations) OR node is right child of its parent and parent is also right child of grand parent (Two Left Rotations).

- Zig-Zag and Zag-Zig. Node is left child of parent and parent is right child of grand parent (Left Rotation followed by right rotation) OR node is right child of its parent and parent is left child of grand parent (Right Rotation followed by left rotation).

- Zig-Zig and Zag-Zag. Node is left child of parent and parent is also left child of grand parent (Two right rotations) OR node is right child of its parent and parent is also right child of grand parent (Two Left Rotations).
Insertion
To insert a value x into a splay tree:
- Insert x as with a normal binary search tree.
- when an item is inserted, a splay is performed.
- As a result, the newly inserted node x becomes the root of the tree.
Deletion
To delete a node x, use the same method as with a binary search tree: if x has two children, swap its value with that of either the rightmost node of its left sub tree (its in-order predecessor) or the leftmost node of its right subtree (its in-order successor). Then remove that node instead. In this way, deletion is reduced to the problem of removing a node with 0 or 1 children. Unlike a binary search tree, in a splay tree after deletion, we splay the parent of the removed node to the top of the tree.
Advantages
Good performance for a splay tree depends on the fact that it is self-optimising, in that frequently accessed nodes will move nearer to the root where they can be accessed more quickly. The worst-case height—though unlikely—is O(n), with the average being O(log n). Having frequently used nodes near the root is an advantage for many practical applications (also see Locality of reference), and is particularly useful for implementing caches and garbage collection algorithms.
Advantages include:
- Comparable performance: Average-case performance is as efficient as other trees.
- Small memory footprint: Splay trees do not need to store any bookkeeping data.
Disadvantages
The most significant disadvantage of splay trees is that the height of a splay tree can be linear. For example, this will be the case after accessing all n elements in non-decreasing order. Since the height of a tree corresponds to the worst-case access time, this means that the actual cost of an operation can be high. However the amortised access cost of this worst case is logarithmic, O(log n). Also, the expected access cost can be reduced to O(log n) by using a randomised variant.
The representation of splay trees can change even when they are accessed in a 'read-only' manner (i.e. by find operations). This complicates the use of such splay trees in a multi-threaded environment. Specifically, extra management is needed if multiple threads are allowed to perform find operations concurrently. This also makes them unsuitable for general use in purely functional programming, although even there they can be used in limited ways to implement priority queues.
References
https://en.wikipedia.org/wiki/Splay_tree
https://github.com/xorz57/forest
https://github.com/InamTaj/data-structures
