Lab Exercise 8 - Recursion

In this exercise we will implement the Quicksort algorithm using recursive functions. As with earlier sort algorithms, we will implement a generic quickSort algorithm that operates on a pair of bi-directional iterators.

Quicksort

Quicksort is a fast sorting algorithm, which is used not only for educational purposes, but also widely applied in practice. On the average, it has O(n log n) complexity, making quicksort suitable for sorting big data volumes.

Algorithm

A divide-and-conquer strategy is used in quicksort.

Choose a pivot value. We take the value of the middle element as pivot value, but it can be any value, which is in range of sorted values, even if it is not present in the array. Note that in our implementation, we take the easy option of using the first value in the range specified as the pivot value. Assuming the input data set is unsorted, this is just as valid as a median pivot value, and makes the implementation a bit simpler.
Partition. Rearrange elements in such a way, that all elements which are lesser than the pivot go to the left part of the array and all elements greater than the pivot, go to the right part of the array. Values equal to the pivot can stay in any part of the array. Notice, that array may be divided in non-equal parts.
Sort both parts. Apply quicksort algorithm recursively to the left and the right parts.

Partition algorithm in detail

There are two indices i and j and at the very beginning of the partition algorithm i points to the first element in the array and j points to the last one. Then algorithm moves i forward, until an element with value greater or equal to the pivot is found. Index j is moved backward, until an element with value lesser or equal to the pivot is found. If i ≤ j then they are swapped and i steps to the next position (i + 1), j steps to the previous one (j - 1). Algorithm stops, when i becomes greater than j.

After partition, all values before i-th element are less or equal than the pivot and all values after j-th element are greater or equal to the pivot.

Example. Sort {1, 12, 5, 26, 7, 14, 3, 7, 2} using quicksort.
quick-sort

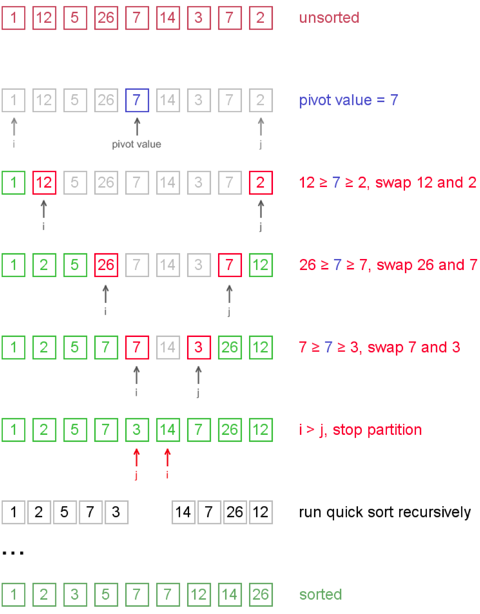
Notice, that we show here only the first recursion step, in order not to make example too long. But, in fact, {1, 2, 5, 7, 3} and {14, 7, 26, 12} are sorted then recursively.

Exercise

Open the sort project we created in Lab 3, and add the Quicksort algorithm implementation (header) and unit test suite (source) files to the project. Run the project as normal and verify the implementation.

quicksort.h

Quicksort algorithm implementation

#pragma once

namespace csc240
{
  namespace internal
  {
    template <typename Iterator, typename Comparator>
    Iterator partition( Iterator first, Iterator last, Comparator comparator )
    {
      auto mid = first;
      auto pivot = *( first++ );
      std::advance( last, -1 );

      while ( first <= last )
      {
        while ( comparator( *first, pivot ) && ( first != last ) )
        {
          std::advance( first, 1 );
        }
        while ( comparator( pivot, *last ) ) std::advance( last, -1 );
        if ( first >= last ) break;

        std::iter_swap( first, last );
        std::advance( first, 1 );
      }

      std::iter_swap( mid, last );
      return last;
    }
  }

  template <typename Iterator, typename Comparator = 
    std::less<typename std::iterator_traits<Iterator>::value_type>>
  void quickSort( Iterator first, Iterator last, Comparator comparator = {} )
  {
    if ( std::distance( first, last ) < 2 ) return;

    auto pivot = internal::partition( first, last, comparator );
    quickSort( first, pivot, comparator );
    quickSort( pivot + 1, last, comparator );
  }
}

Point.h

A simple data object to use to test sorting custom objects.

#pragma once

#include <ostream>

#define POINT_VALUES {\
 csc240::Point{1.0, 0.0},\
 csc240::Point{0.0, 1.0 },\
 csc240::Point{1.0, 1.0},\
 csc240::Point{0.0, 0.0 },\
 csc240::Point{2.0, 2.0} \
}
#define POINT_RESULTS {\
 csc240::Point{0.0, 0.0},\
 csc240::Point{0.0, 1.0 },\
 csc240::Point{1.0, 0.0},\
 csc240::Point{1.0, 1.0 },\
 csc240::Point{2.0, 2.0}\
}

namespace csc240
{
  struct Point { double x; double y; };

  inline std::ostream& operator << ( std::ostream& stream, const Point& point )
  {
    stream << "Point - x: " << point.x << ", y: " << point.y << std::endl;
    return stream;
  }

  inline bool operator == ( const Point& left, const Point& right )
  {
    return ( left.x == right.x ) && ( left.y == right.y );
  }

  inline bool operator != ( const Point& left, const Point& right )
  {
    return !( left == right );
  }

  inline bool operator < ( const Point& left, const Point& right )
  {
    return ( ( left.x == right.x ) ? ( left.y < right.y ) : ( left.x < right.x ) );
  }

  inline bool operator > ( const Point& left, const Point& right )
  {
    return ( ( left.x == right.x ) ? ( left.y > right.y ) : ( left.x > right.x ) );
  }
}

quicksort.cpp

Unit test suite (same tests are for other sort algorithms) for our Quicksort implementation.

#include "catch.hpp"
#include "quicksort.h"
#include "common.h"
#include "Point.h"

#include<array>
#include <iterator>
#include<vector>

SCENARIO( "Quicksort can sort numbers" )
{
  GIVEN( "An array of integers" )
  {
    int array[] = INT_VALUES;
    const int results[] = INT_RESULTS;

    THEN( "Sorted array matches expected result" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ) );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::cbegin( results ) ) );
    }

    AND_THEN( "Sorted array matches expected result when ordered in descending order" )
    {
      csc240::quickSort( std::rbegin( array ), std::rend( array ) );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::crbegin( results ) ) );
    }

    AND_THEN( "Sorted array matches expected result when using a less than lambda" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ),
        [] ( int lhs, int rhs ) { return lhs < rhs; } );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::cbegin( results ) ) );
    }

    AND_THEN( "Sorted array matches expected result when using a greater than lambda" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ),
        [] ( int lhs, int rhs ) { return lhs > rhs; } );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::crbegin( results ) ) );
    }
  }
}

SCENARIO( "Quicksort can sort text" )
{
  GIVEN( "An array of strings" )
  {
    std::array<std::string, 4> array STRING_VALUES;
    const std::array<std::string, 4> results STRING_RESULTS;

    THEN( "Sorted array matches expected result" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ) );
      REQUIRE( array == results );
    }

    AND_THEN( "Sorted array matches expected result when ordered in descending order" )
    {
      csc240::quickSort( std::rbegin( array ), std::rend( array ) );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::crbegin( results ) ) );
    }

    AND_THEN( "Sorted array matches expected result when using a less than lambda" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ),
        [] ( const std::string& lhs, const std::string& rhs ) { return lhs < rhs; } );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::cbegin( results ) ) );
    }

    AND_THEN( "Sorted array matches expected result when using a greater than lambda" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ),
        [] ( const std::string& lhs, const std::string& rhs ) { return lhs > rhs; } );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::crbegin( results ) ) );
    }
  }
}

SCENARIO( "Quicksort can sort custom objects" )
{
  GIVEN( "A vector of Point objects" )
  {
    std::vector<csc240::Point> vector POINT_VALUES;
    const std::vector<csc240::Point> results POINT_RESULTS;

    THEN( "Sorted vector matches expected result" )
    {
      csc240::quickSort( vector.begin(), vector.end() );
      REQUIRE( vector == results );
    }

    AND_THEN( "Sorted vector matches expected result when using a less than lambda" )
    {
      csc240::quickSort( std::begin( vector ), std::end( vector ),
        [] ( const csc240::Point& lhs, const csc240::Point& rhs ) { return lhs < rhs; } );
      REQUIRE( std::equal( std::cbegin( vector ), std::cend( vector ),
        std::cbegin( results ) ) );
    }

    AND_THEN( "Sorted array matches expected result when using a greater than lambda" )
    {
      csc240::quickSort( std::begin( vector ), std::end( vector ),
        [] ( const csc240::Point& lhs, const csc240::Point& rhs ) { return lhs > rhs; } );
      REQUIRE( std::equal( std::cbegin( vector ), std::cend( vector ),
        std::crbegin( results ) ) );
    }
  }

  GIVEN( "A vector of Point objects" )
  {
    std::vector<csc240::Point> vector POINT_VALUES;
    std::vector<csc240::Point> results POINT_VALUES;
    std::sort( results.begin(), results.end() );

    THEN( "Sorted vector matches std::sort" )
    {
      csc240::quickSort( vector.begin(), vector.end() );
      REQUIRE( vector == results );
    }
  }
}

SCENARIO( "Quicksort implementation leaves pre-sorted data intact" )
{
  GIVEN( "A pre-sorted array of integers" )
  {
    int array[] = INT_RESULTS;
    const int results[] = INT_RESULTS;

    THEN( "Sorted array matches expected result" )
    {
      csc240::quickSort( std::begin( array ), std::end( array ) );
      REQUIRE( std::equal( std::cbegin( array ), std::cend( array ),
        std::cbegin( results ) ) );
    }
  }
}

Why does it work?

On the partition step algorithm divides the array into two parts and every element a from the left part is less or equal than every element b from the right part. Also a and b satisfy a ≤ pivot ≤ b inequality. After completion of the recursion calls both of the parts become sorted and, taking into account arguments stated above, the whole array is sorted.